栈
定义
栈(stack)是一个有序线性表,只能在表的一端(栈顶,top)执行插入和删除操作。最后插入的元素将第一个被删除。所以,栈也称为后进先出(Last In First Out, LIFO),或先进后出(First In Last Out, FILO)线性表。
两个改变栈操作都有专用名称。一个称为入栈(push),表示在栈中插入一个元素;另一个称为出栈(pop),表示从栈中删除一个元素。
试图对一个空栈执行出栈操作称为下溢(underflow);试图对一个满栈执行入栈操作称为溢出(overflow),通常,下溢和溢出均认为是异常。
抽象数据结构
栈的数据结构如下图所示:
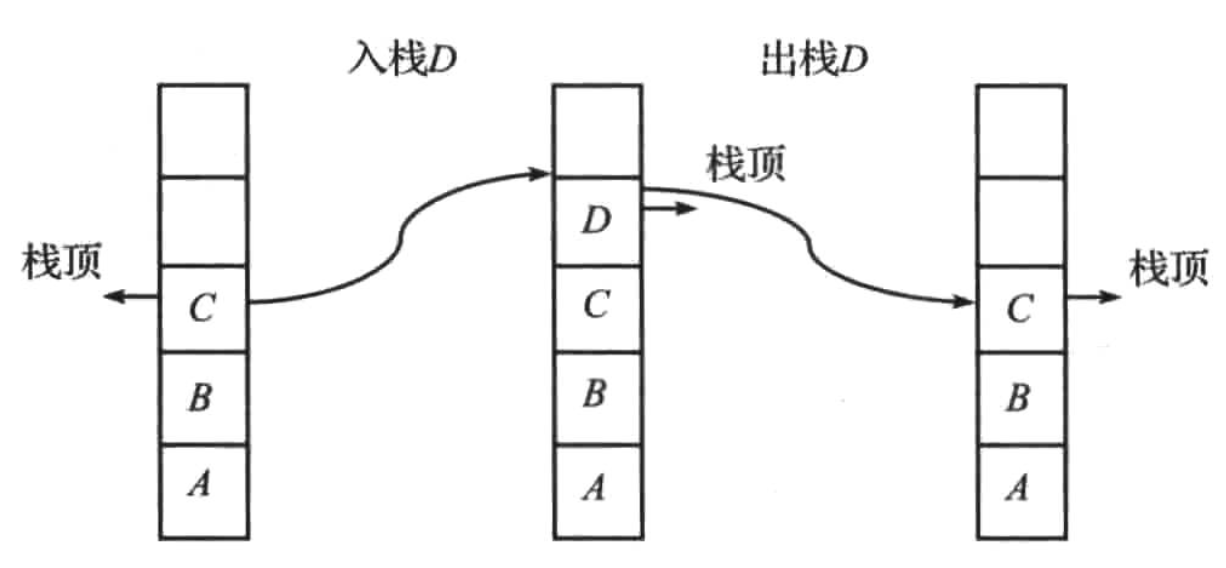
栈的主要操作:
- void push(Object data):将data(数据)插入栈
- Object pop():删除并返回最后一个插入栈的元素
栈的辅助操作:
- Object top():返回最后一个插入栈的元素,但不删除
- int size():返回存储在栈中元素的个数
- boolean isEmpty():判断栈中是否有元素
- boolean isFull():判断栈中元素是否已存满
异常
在栈抽象数据类型中,当栈中无元素时不能执行top()和pop()操作,否则会抛出下溢(underflow)异常;当栈中元素已满时不能执行push()操作,否则会抛出溢出(overflow)异常
实现
栈抽象数据类型有多种实现方式。常用的方法包括:
- 基于简单数组的实现方法
- 基于动态数组的实现方法
- 基于链表的实现方法
简单数组实现
概述
如下图所示,从左至右向数组中添加所有的元素,并定义一个变量用来记录数组当前栈顶(top)元素的下标
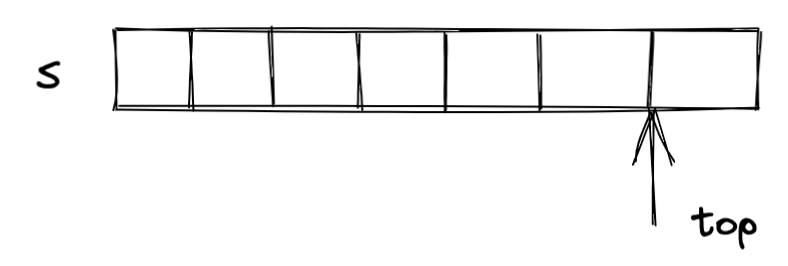
异常
当数组存满了栈元素时,执行入栈(插入元素)操作将抛出栈满异常。当对一个没有存储栈元素的数组执行出栈(删除元素)操作时,将抛出栈空异常
类型声明方式
[!Tip]
本节源代码见Github链接🔗
【👉🏻>>点击展开查看代码】
/**
* 简单数组实现栈
*
* @className: ArrayStack 简单数组实现栈
* @author: Max Solider
* @date: 2022-11-10 15:50
*/public class ArrayStack {
/**
* 栈顶元素下标
*/
private int top;
/**
* 栈容量
*/
private int capacity;
/**
* 用于存储栈元素
*/
private int[] array;
public ArrayStack() {
capacity = 1;
array = new int[capacity];
top = -1;
}
/**
* 栈中是否没有元素
*
* @return false:有元素,true:无元素
*/
public boolean isEmpty() {
return top == -1;
}
/**
* 栈中是否已存满元素
*
* @return false:未存满,true:已存满
*/
public boolean isFull() {
return top == capacity - 1;
}
/**
* 向栈中插入元素
*
* @param data 待插入元素
*/
public void push(int data) {
if (isFull()) {
System.out.println("Stack Overflow.");
return; }
top++;
array[top] = data;
System.out.println("Stack push success.");
}
/**
* 取出栈顶元素,并从栈中删除
*
* @return 栈顶元素
*/
public int pop() {
if (isEmpty()) {
System.out.println("Stack is empty.");
return 0;
}
int result = array[top];
top--;
return result;
}
/**
* 删除栈
*/
public void deleteStack() {
top = -1;
}
}
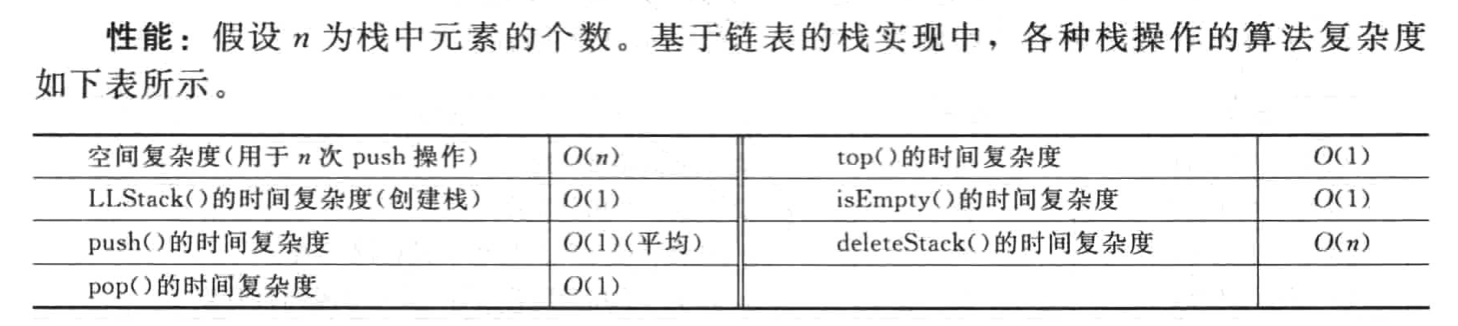
性能
假设n为栈中元素的个数,在基于简单数组的栈实现中,各种栈操作的算法复杂度如下表所示:

局限性
栈的最大空间必须预先声明且不能改变。试图对一个满栈执行入栈操作将产生一个针对简单数组这种特定实现栈方式的异常。
动态数组实现
概述
要解决在固定大小的数组中,如何处理所有空间都已经保存了栈元素这种情况,有两种方法:
解决方案一
当栈满时,每次入栈时将数组的大小增加1,出栈时将数组大小减少1。这种方案开销较大,每次对满栈执行插入操作时,都需要新建一个大小为的数组,将老数组中的元素复制到新数组中。在执行m次push操作后,总时间开销T(m)为
解决方案二
使用数组倍增来提高性能,减少数组复制次数。如果数组空间已满,新建一个比原数组空间大一倍的新数组,然后复制元素。当执行n次push操作时,需要执行的复制操作次数(即倍增操作次数)为次。这样执行n次push操作的时间开销为
即T(n)为O(n),一次push操作的平摊时间为O(1)。
类型声明方式
[!Tip]
本节源代码见Github链接🔗
【👉🏻>>点击展开查看代码】
/**
* 动态数组实现栈
*
* @className: DynArrayStack
* @author: Max Solider
* @date: 2022-11-11 11:40
*/
public class DynArrayStack {
/**
* 栈顶元素下标
*/
private int top;
/**
* 栈容量
*/
private int capacity;
/**
* 用于存放栈元素的数组
*/
private int[] array;
public DynArrayStack() {
capacity = 1;
array = new int[capacity];
top = -1;
}
/**
* 栈内是否没有数据
*
* @return true:没有数据;false:有数据
*/
public boolean isEmpty() {
return top == -1;
}
/**
* 栈内数据是否已存满
*
* @return true:已存满;false:未存满
*/
public boolean isFull() {
return top == capacity - 1;
}
/**
* 插入元素
*
* @param data 待插入元素
*/
public void push(int data) {
if (isFull()) {
doubleStack();
}
top++;
array[top] = data;
}
/**
* 弹出栈顶元素
*
* @return 栈顶元素
*/
public int pop() {
if (isEmpty()) {
System.out.println("Stack Overflow.");
return 0;
}
int result = array[top];
top--;
return result;
}
/**
* 删除栈
*/
public void deleteStack() {
top = -1;
}
/**
* 数组倍增
*/
private void doubleStack() {
int newArray[] = new int[capacity * 2];
System.arraycopy(array, 0, newArray, 0, capacity);
capacity = capacity * 2;
array = newArray;
}
}
性能

局限性
倍增太多可能导致内存溢出
链表实现
概述
使用链表也可以实现栈。通过在链表的表头插入元素的方式实现push操作,删除链表的表头结点(栈顶结点)实现pop操作
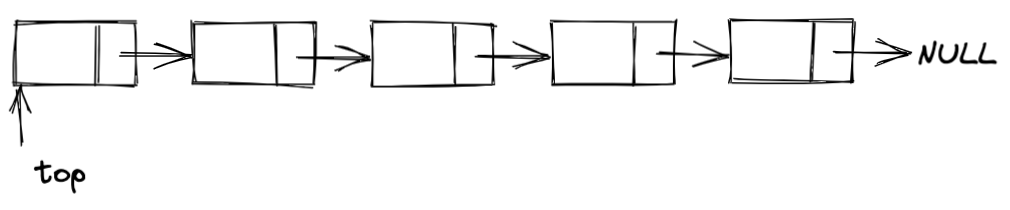
类型声明方式
[!Tip]
本节源代码见Github链接🔗
【👉🏻>>点击展开查看代码】
/**
* 链表实现栈
*
* @className: LLStack
* @author: Max Solider
* @date: 2022-11-11 11:40
*/
public class LLStack {
private LLNode headNode;
public LLStack() {
}
/**
* 栈内是否没有数据
*
* @return true:没有数据;false:有数据
*/
public boolean isEmpty() {
return headNode == null;
}
/**
* 栈内数据是否已存满
*
* @return true:已存满;false:未存满
*/
public boolean isFull() {
return false;
}
/**
* 插入元素
*
* @param data 待插入元素
*/
public void push(int data) {
if (headNode == null) {
headNode = new LLNode(data);
return; }
LLNode newHead = new LLNode(data);
newHead.setNext(headNode);
headNode = newHead;
}
/**
* 弹出栈顶元素
*
* @return 栈顶元素
*/
public int pop() {
if (isEmpty()) {
System.out.println("Stack Empty.");
return 0;
}
int result = headNode.getData();
headNode = headNode.getNext();
return result;
}
/**
* 删除栈
*/
public void deleteStack() {
headNode = null;
}
/**
* 链表结点
*/
private class LLNode {
/**
* 结点元素
*/
private int data;
/**
* 后继指针
*/
private LLNode next;
public LLNode(int data) {
this.data = data;
}
public LLNode getNext() {
return next;
}
public void setNext(LLNode next) {
this.next = next;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
}
}
性能
栈的各种实现方法比较
递增策略和倍增策略的比较
通过分析完成n个push操作的总时间开销T(n)来比较递增策略和倍增策略的区别。从长度为1的数组表示的空栈开始,一次push操作的平摊时间等于一组push操作的总时间开销的平均值,记为T(n)/n。
递增策略:实现push操作的平摊时间开销为
倍增策略:实现push操作的平摊时间开销为
基于数组实现和基于链表实现的比较
基于数组实现的栈:
- 各个操作都是常数时间开销
- 每隔一段时间倍增操作的开销较大
- (从空栈开始)n个操作的任意序列的平摊时间开销为O(n)
基于链表实现的栈:
- 栈规模的增加和减小都很简洁
- 各个操作都是常数时间开销
- 每个操作都要使用额外的空间和时间开销来处理指针
常见问题
关于栈的常见问题见 01-常见问题