判定链表中是否存在环
[!Tip]
本节源代码见Github链接🔗
问题描述
判定给定的链表是以NULL结尾,还是形成一个环
核心思路
通过Floyd环判定算法🔗来解决。主要包含以下3步:
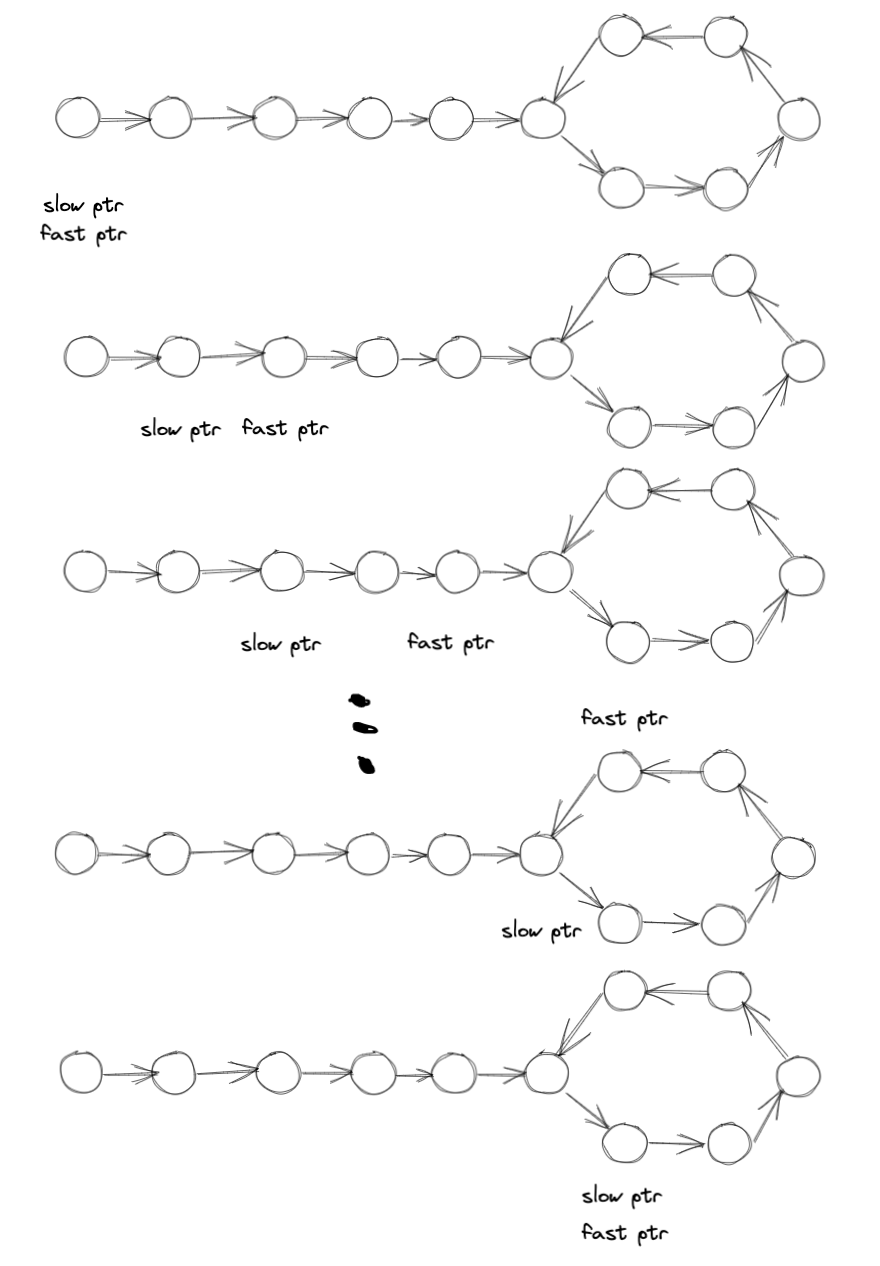
- 定义两个指向链表头结点的指针slowPtr和fastPtr;
- 将两个指针按照不同的速度进行移动,如slowPtr每次向后移动1个结点,fastPtr每次向后移动2个结点;
- 若链表中存在环,slowPtr和fastPtr终将指向同一结点;若不存在环,fastPtr会先指向NULL。
Floyd环判定算法,又称为龟兔赛跑算法,可以判断在有限状态机、迭代函数或者链表上是否存在环,并能判断环的起点与长度。 如果有限状态机、迭代函数或者链表上存在环,那么在某个环上以不同速度前进的2个指针必定会在某个时刻相遇。同理,如果从同一个起点(即使这个起点不在环上),同时开始以不同的速度前进的2个指针最终相遇,那么可以判定存在一个环,且可以求出二者相遇处所在的环的起点与长度。
实现代码
【👉🏻>>点击展开查看代码】
/**
* 判断链表中是否存在环
*
* @param headNode
* @return boolean
* @author: Max Solider
* @date: 2022/10/9 14:18
*/
boolean doesLinkedListContainsLoop(NormalListNode headNode) {
if (headNode == null || headNode.getNext() == null) {
return false;
}
NormalListNode slowPtr = headNode, fastPtr = headNode;
while (fastPtr.getNext() != null && fastPtr.getNext().getNext() != null) {
fastPtr = fastPtr.getNext().getNext();
slowPtr = slowPtr.getNext();
if (slowPtr == fastPtr) {
System.out.println("There is a loop in the linked list.");
return true; }
}
System.out.println("There is no loop in the linked list.");
return false;
}
时间复杂度
时间复杂度为O(n),用于遍历链表。
空间复杂度
空间复杂度为O(1),用于存储临时变量。