树
定义
树是一种类似于链表的数据结构,不过链表的结点是以线性方式简单地指向其后继结点,而树的一个结点可以指向许多个结点。树是一种典型的非线性结构。树结构是表达具有层次特性的图结构的一种方法。 对于树ADT(抽象数据类型),元素的顺序不是考虑的重点。如果需要用到元素的顺序信息,那么可以使用链表、栈、队列等线性数据结构。
术语
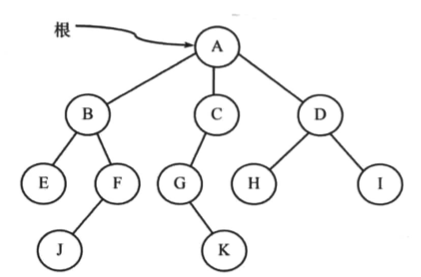
- 根结点:根结点是没有父结点的结点,一棵树中最多有一个根结点
- 边:边表示从父结点到子结点的连接
- 叶子结点:没有子结点的结点叫做叶子结点
- 兄弟结点:有相同父结点的所有结点叫做兄弟结点
- 祖先结点:如果存在一条从根结点到结点q的路径,且结点p出现在这条路径上,那么就可以把结点p叫做结点q的祖先结点,结点q也叫做p的子孙结点
- 结点的大小:结点的大小是指子孙的个数,包括其自身
- 树的层:位于相同深度的所有结点的集合叫做树的层。根结点位于0层
- 结点的深度:是指从根结点到该结点的路径长度
- 结点的高度:是指从该结点到最深结点的路径长度
- 树的高度:是树中所有结点高度的最大值,树的深度是树中所有结点深度的最大值。对于同一棵树,其深度和高度是相同的,但是对于各个结点,其深度和高度不一定相同
- 斜树:如果树中除了叶子结点外,其余每一结点只有一个子结点,则这种树称作斜树。对于每个结点仅有一个左子结点的树叫做左斜树。只有一个右子结点的树叫做右斜树
二叉树
定义
如果一棵树中的每个结点有0、1或者2个子结点,那么这棵树就称为二叉树。空树也是一棵有效的二叉树。
二叉树的类型
- 严格二叉树:二叉树中的每个结点要么有两个子结点,要么没有子结点
- 满二叉树:二叉树中的每个结点恰好有两个子结点且所有叶子结点都在同一层(满二叉树的叶子结点个数是2^h)
- 完全二叉树:所有叶子结点的深度为h或h-1
二叉树的数据结构
【👉🏻>>点击展开查看代码】
/**
* 二叉树
*
* @className: BinaryTreeNode
* @author: Max Solider
* @date: 2023-06-11 11:29
*/public class BinaryTreeNode {
private int data;
private BinaryTreeNode left;
private BinaryTreeNode right;
public int getData() {
return data;
}
public BinaryTreeNode getLeft() {
return left;
}
public BinaryTreeNode getRight() {
return right;
}
public void setData(int data) {
this.data = data;
}
public void setLeft(BinaryTreeNode left) {
this.left = left;
}
public void setRight(BinaryTreeNode right) {
this.right = right;
}
}
二叉树的操作
- 基本操作
- 向树中插入一个元素
- 从树中删除一个元素
- 查找一个元素
- 遍历树
- 辅助操作
- 编译器中的表达式树
- 用于数据压缩算法中的赫夫曼编码树
- 支持在集合中查找、插入和删除,其平均时间复杂度为O(logn)的二叉搜索树(BST)
- 优先队列(PQ),它支持以对数时间对集合中的最小(或最大)数据元素进行搜索和删除
二叉树的遍历
基于当前结点(D)、左子结点(L)、右子结点(R)的访问顺序,可以分为: - 前序遍历(DLR)
- 中序遍历(LDR)
- 后序遍历(LRD)
- 层次遍历
【👉🏻>>点击展开查看代码】
/**
* 前序遍历二叉树
*
* @param treeNode 二叉树
*/
public static void preOrder(BinaryTreeNode treeNode) {
if (treeNode == null) {
return;
}
System.out.println(treeNode.getData());
preOrder(treeNode.getLeft());
preOrder(treeNode.getRight());
}
/**
* 中遍历二叉树
*
* @param treeNode 二叉树
*/
public static void inOrder(BinaryTreeNode treeNode) {
if (treeNode == null) {
return;
}
inOrder(treeNode.getLeft());
System.out.println(treeNode.getData());
inOrder(treeNode.getRight());
}
/**
* 后序遍历二叉树
*
* @param treeNode 二叉树
*/
public static void postOrder(BinaryTreeNode treeNode) {
if (treeNode == null) {
return;
}
postOrder(treeNode.getLeft());
postOrder(treeNode.getRight());
System.out.println(treeNode.getData());
}
/**
* 层次遍历二叉树
*
* @param treeNode 二叉树
*/
public static void levelOrder(BinaryTreeNode treeNode) {
if (treeNode == null) {
return;
}
// 借助队列实现
ArrayQueue queue = new ArrayQueue(20);
queue.enQueue(treeNode);
while (!queue.isEmpty()) {
BinaryTreeNode tmp = (BinaryTreeNode) queue.deQueue();
System.out.println(tmp.getData());
if (tmp.getLeft() != null) {
queue.enQueue(tmp.getLeft());
}
if (tmp.getRight() != null) {
queue.enQueue(tmp.getRight());
}
}
}
常见问题
关于队列的常见问题见 01-常见问题