队列
定义
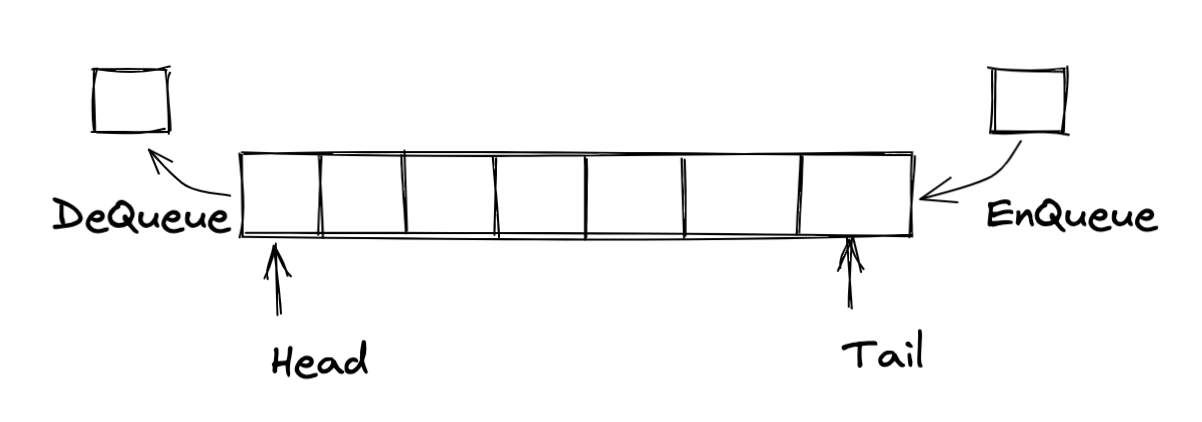
队列是一种只能在一端插入(队尾),在另一端删除(队首)的有序线性表。队列中第一个插入的元素也是第一个被删除的元素。所以,队列是一种先进先出(FIFO)或后进后出(LILO)线性表
与栈类似,两个改变队列操作都有专用名称。一个称为入队(EnQueue),表示在队列中插入一个元素;另一个称为出队(DeQueue),表示从队列中删除一个元素。
试图对一个空队列执行出队操作称为下溢(underflow);试图对一个满队列执行入队操作称为溢出(overflow),通常,下溢和溢出均认为是异常。
抽象数据结构
队列的数据结构如下图所示:
队列的主要操作:
- void enQueue(Object data):将data(数据)插入队列队尾
- Object deQueue():删除并返回队首元素
队列的辅助操作:
- Object front():返回队首元素,但不删除
- int size():返回存储在队列中元素的个数
- boolean isEmpty():判断队列中是否有元素
- boolean isFull():判断队列中元素是否已存满
异常
在队列抽象数据类型中,当队列中无元素时不能执行deQueue()和front()操作,否则会抛出下溢(underflow)异常;当队列中元素已满时不能执行enQueue()操作,否则会抛出溢出(overflow)异常
实现
队列抽象数据类型有多种实现方式。常用的方法包括:
- 基于简单循环数组的实现方法
- 基于动态循环数组的实现方法
- 基于链表的实现方法
简单循环数组实现
概述 之所以选择循环数组来实现队列,而不是选择数组来实现,是为了避免元素出队后对数组中靠前的空间造成浪费。使用循环数组可以有效利用出队后的空闲空间。
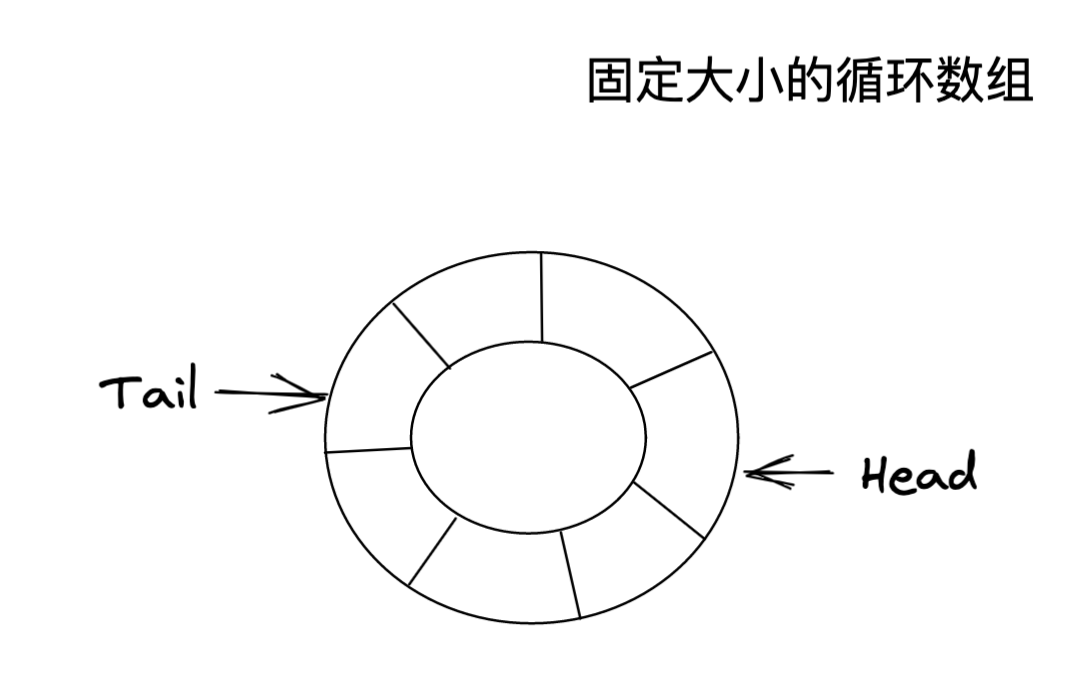
异常 使用循环数组来存储队列中的元素,可能会出现数组被填满的情况,当队列存满了元素时,执行入队(插入元素)操作将抛出队满异常。当对一个没有存储元素的队列执行出队(删除元素)操作时,将抛出空异常
类型声明方式
[!Tip]
本节源代码见Github链接🔗
【👉🏻>>点击展开查看代码】
/**
* 简单循环数组实现队列
*
* @className: ArrayQueue
* @author: Max Solider
* @date: 2023-06-10 15:07
*/public class ArrayQueue {
/**
* 用于存放元素的数组
*/
private int[] array;
/**
* 队首下标
*/
private int head;
/**
* 队尾下标
*/
private int tail;
/**
* 队列容量
*/
private int capacity;
/**
* 初始化队列
* @param size 队列大小
*/
public ArrayQueue(int size) {
capacity = size;
array = new int[size];
head = -1;
tail = -1;
}
/**
* 创建简单循环数组队列
* @param size 队列大小
* @return 队列
*/
public static ArrayQueue createArrayQueue(int size) {
return new ArrayQueue(size);
}
/**
* 判断队列中是否没元素
* @return true,false
*/ public boolean isEmpty() {
return head == -1;
}
/**
* 判断队列中是否已满
* @return true,false
*/ public boolean isFull() {
return (tail + 1) % capacity == head;
}
/**
* 获取队列中元素个数
* @return 元素个数
*/
public int getQueueSize() {
return (capacity - head + tail + 1) % capacity;
}
/**
* 入队
* @param data 待入队元素
*/
public void enQueue(int data) {
if (isFull()) {
return;
}
if (head == -1) {
head = tail = 0;
} else {
tail = (tail + 1) % capacity;
}
array[tail] = data;
}
/**
* 出队
* @return 队首元素
*/
public Integer deQueue() {
if (isEmpty()) {
return null;
}
int result = array[head];
if (head == tail) {
head = tail = -1;
} else {
head = (head + 1) % capacity;
}
return result;
}
public void print() {
if (tail >= head) {
for (int i = head; i
性能
假设n为队列中元素的个数,在基于简单循环数组的队列实现中,各种队列操作的算法复杂度如下表所示:

局限性
队列的最大空间必须预先声明且不能改变。试图对一个满队列执行入队操作将产生一个针对简单数组这种特定实现队列方式的异常。
动态循环数组实现
概述 动态循环数组的思路是,在每次元素入队时,判断队列是否已满,如队列已满,则创建一个容量是原队列容量两倍的队列,并将原队列中的元素复制到新队列中
局限性 倍增太多可能导致内存溢出
链表实现
概述 使用链表实现队列,每次元素入队时在链表尾插入元素,元素出队时删除链表表头元素
队列的各种实现方法比较
基于数组实现和基于链表实现的比较
基于数组实现的队列:
- 各个操作都是常数时间开销
- 每隔一段时间倍增操作的开销较大
- (从空队列开始)n个操作的任意序列的平摊时间开销为O(n)
基于链表实现的队列:
- 队列规模的增加和减小都很简洁
- 各个操作都是常数时间开销
- 每个操作都要使用额外的空间和时间开销来处理指针
常见问题
关于队列的常见问题见 01-常见问题