双向链表
[!Tip]
本节源代码见Github链接🔗
概述
在双向链表中,每个元素结点保存了指向前驱结点的指针。因此对于任意一个结点,都可以从两个方向进行操作。
双向链表的数据结构如下图所示:
 双向链表的类型声明方式如下所示:
双向链表的类型声明方式如下所示:
【👉🏻>>点击展开查看代码】
/**
* 双向链表元素结点数据结构
*
* @className: DllNode
* @author: Max Solider
* @date: 2022-10-08 17:02
*/
public class DllNode {
/**
* 结点数据
*/
private int data;
/**
* 前驱结点
*/
private DllNode previous;
/**
* 后继结点
*/
private DllNode next;
public DllNode(int data) {
this.data = data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public DllNode getPrevious() {
return previous;
}
public void setPrevious(DllNode previous) {
this.previous = previous;
}
public DllNode getNext() {
return next;
}
public void setNext(DllNode next) {
this.next = next;
}
}
优缺点及相关应用场景
优点:
- 对于链表中的任意结点,可以快速后退到前驱结点。
缺点:
- 每个结点需要额外的内存开销,用于保存前驱结点;
- 对结点的插入和删除更加费时(需要更多的指针操作)。
应用:
基本操作
对双向链表的基本操作包括:
- 在链表中插入元素结点;
- 删除链表中的元素结点。
在链表中插入元素
常见操作:
- 在链表开头前插入一个新结点;
- 在链表尾后插入一个新结点;
- 在链表中间任意位置插入一个新结点。
在表头前插入一个新结点
核心思路:
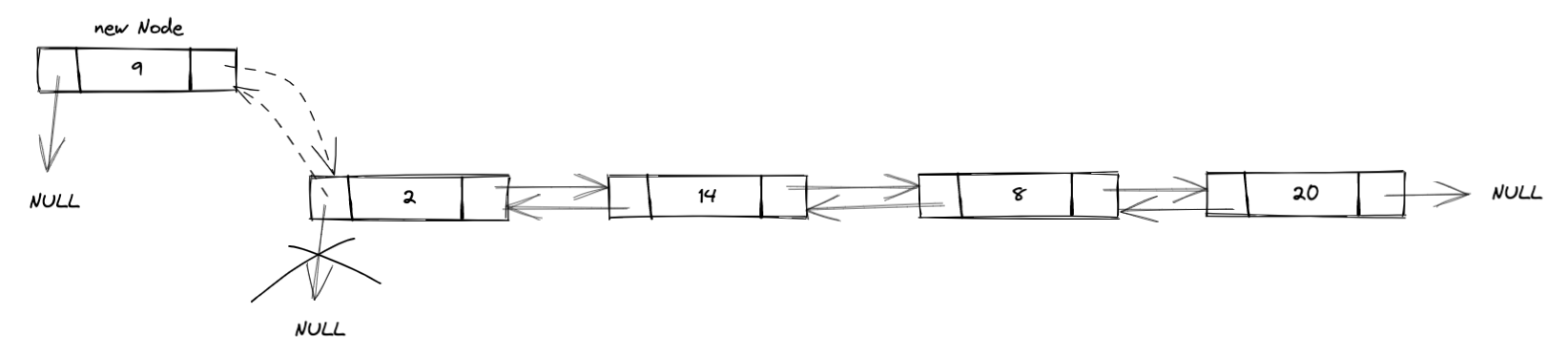
在双向链表的表头前插入一个新结点,包括以下2步:
- 将原链表头的前驱指针指向新结点;
- 将新结点的后继指针指向原表头结点,并将新结点的前驱指针赋值为NULL。
实现代码:
【👉🏻>>点击展开查看代码】
/**
* 在双向链表头前插入新结点
*
* @param headNode 原链表头结点
* @param newNode 新结点
* @return DllNode
* @author: Max Solider
* @date: 2022/10/8 17:12
*/
DllNode insertHead(DllNode headNode, DllNode newNode) {
if (newNode == null) {
return headNode;
}
if (headNode == null) {
return newNode;
}
// 改变原头结点的前驱指针
headNode.setPrevious(newNode);
// 改变新结点的后继指针
newNode.setNext(headNode);
headNode = newNode;
return headNode;
}
时间复杂度:
时间复杂度是O(1)。
空间复杂度:
无需额外空间。
在表尾插入一个新结点
核心思路:
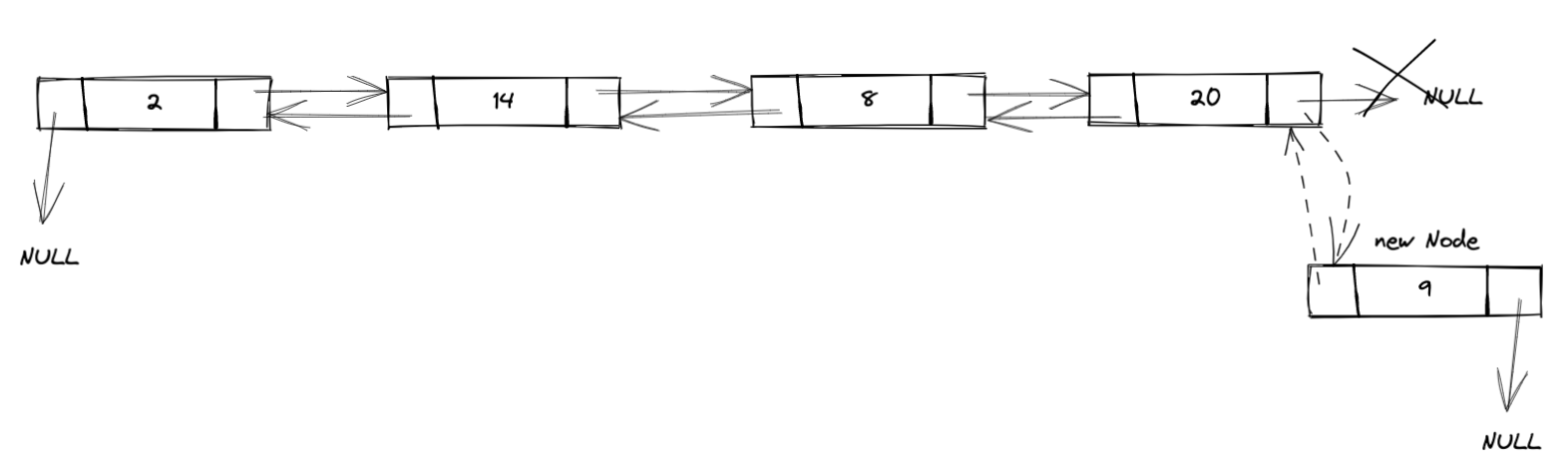
在表尾后插入一个新结点,包含以下3步:
- 遍历找到原表尾结点;
- 将原表尾结点的后继指针指向新结点;
- 将新结点的前驱指针指向原表尾结点,并将后继指针指向NULL。
实现代码:
【👉🏻>>点击展开查看代码】
/**
* 在链表尾后插入新结点
*
* @param headNode 链表头结点指针
* @param newNode 新结点
* @return DllNode 新的表头指针
* @author: Max Solider
* @date: 2022/10/8 17:21
*/
DllNode insertTail(DllNode headNode, DllNode newNode) {
if (headNode == null) {
return newNode;
}
if (newNode == null) {
return headNode;
}
DllNode currentNode = headNode;
while (currentNode.getNext() != null) {
currentNode = currentNode.getNext();
}
currentNode.setNext(newNode);
newNode.setPrevious(currentNode);
newNode.setNext(null);
return headNode;
}
时间复杂度:
由于需要遍历链表,时间复杂度为O(n)
空间复杂度:
需要存储一个临时变量,空间复杂度为O(1)
在链表中间插入一个新结点
核心思路:
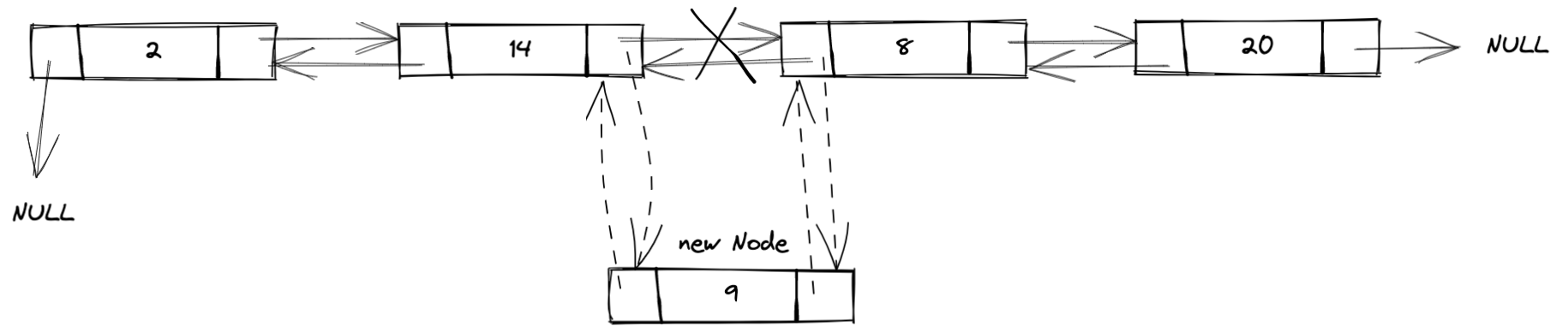
在链表中间任意位置插入一个新结点,包含以下6步:
- 判断插入位置合法性;
- 判断是否在表头插入;
- 遍历找到待插入位置;
- 找到待插入位置原结点的前驱结点,并将前驱结点的后继指针指向新结点;
- 将原结点的前驱指针指向新结点;
- 将新结点的前驱指针指向原前驱结点,将新结点的后继指针指向原结点。
实现代码:
【👉🏻>>点击展开查看代码】
/**
* 双向链表中任意位置插入结点
*
* @param headNode 链表头指针
* @param newNode 新结点
* @param position 待插入位置
* @return DllNode
* @author: Max Solider
* @date: 2022/10/8 17:47
*/
DllNode insert(DllNode headNode, DllNode newNode, int position) {
if (headNode == null) {
headNode = newNode;
return headNode;
}
if (position < 1) {
System.out.println("The position of node to insert is invalid. The position must be greater than 0.");
return headNode;
}
if (position == 1) {
// 改变原头结点的前驱指针
headNode.setPrevious(newNode);
// 改变新结点的后继指针
newNode.setNext(headNode);
headNode = newNode;
return headNode;
}
// 先找到待插入位置的原结点
int count = 1;
DllNode currentNode = headNode;
DllNode previousNode = currentNode.getPrevious();
while (count != position) {
if (currentNode == null) {
System.out.println("The position of node to insert is invalid. The position must be less than " + (count + 1));
return headNode;
}
previousNode = currentNode;
currentNode = currentNode.getNext();
count++;
}
// 改变原结点前驱结点的后继指针
previousNode.setNext(newNode);
// 改变新结点的前驱指针和后继指针
newNode.setPrevious(previousNode);
newNode.setNext(currentNode);
// 如果后继结点不是null,则修改后继结点的前驱指针
if (currentNode != null) {
currentNode.setPrevious(newNode);
}
return headNode;
}
时间复杂度:
因为需要遍历链表,时间复杂度是O(n)。
空间复杂度:
因为需要保存临时变量,空间复杂度为O(1)。
从链表中删除元素
常见操作:
- 删除链表的表头;
- 删除链表的表尾;
- 删除链表中任意结点。
删除表头结点
核心思路:
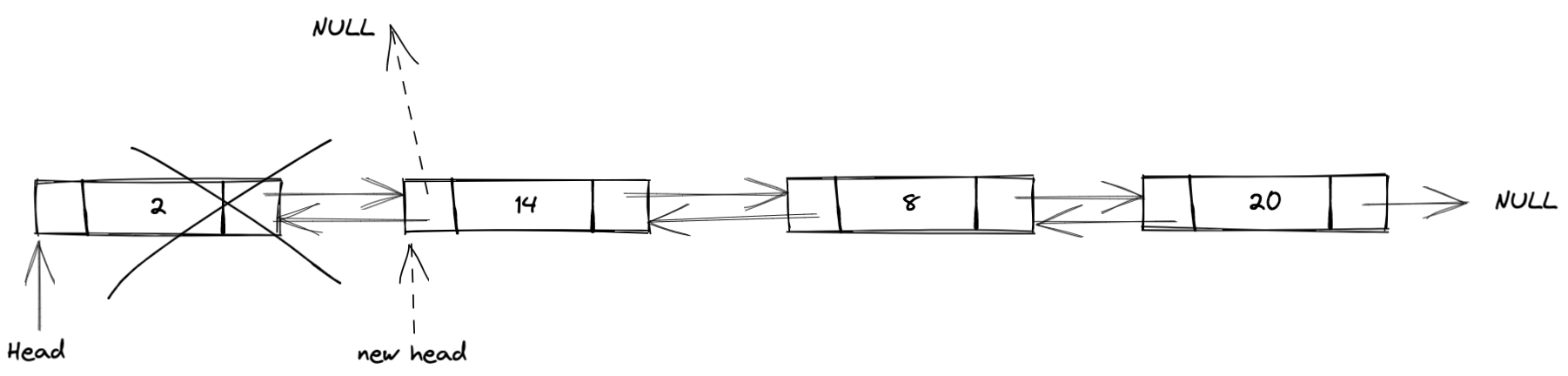
删除表头结点,包含以下4步:
- 将表头指针指向第二个结点;
- 将第二个结点的前驱指针指向NULL;
- 将原表头结点的后继指针指向NULL;
- 移除原表头结点。
实现代码:
【👉🏻>>点击展开查看代码】
/**
* 删除表头结点
*
* @author: Max Solider
* @date: 2022/10/8 19:38
* @param headNode
* @return org.example.linkedlist.dll.DllNode
*/
DllNode deleteHead(DllNode headNode) {
if (headNode == null) {
return headNode;
}
// 如果链表只有一个元素
if (headNode.getNext() == null) {
headNode = null;
return headNode;
}
// 将表头指针指向第二个结点
DllNode newHead = headNode.getNext();
// 修改将原表头结点的后继指针
headNode.setNext(null);
// 修改新表头结点的前驱指针
newHead.setPrevious(null);
headNode = newHead;
return headNode;
}
时间复杂度:
因为无需遍历链表,时间复杂度是O(1)。
空间复杂度:
因为需要保存临时变量,空间复杂度为O(1)。
删除表尾结点
核心思路:
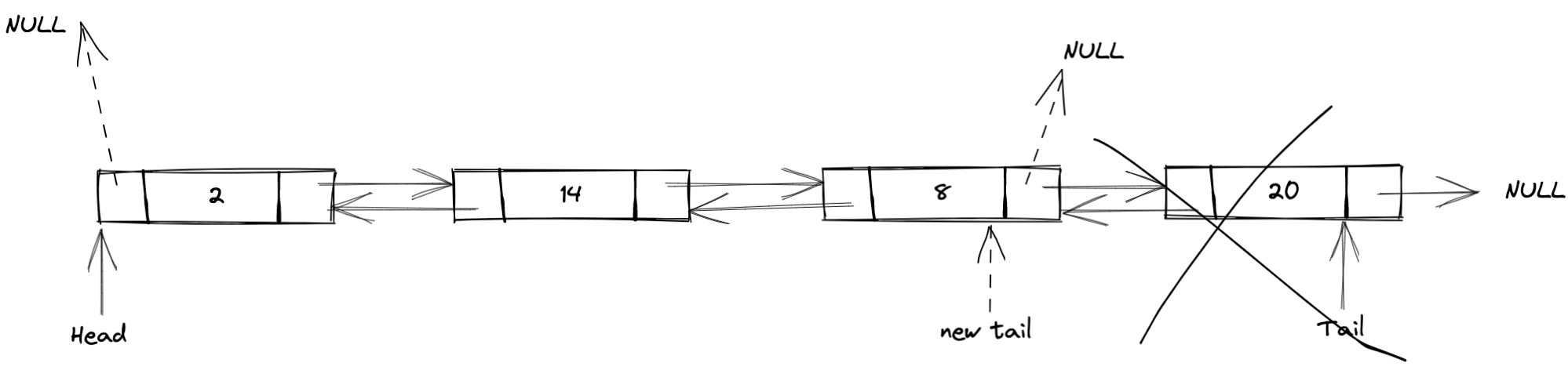
删除表尾结点,包含以下4步:
- 找到原表尾结点;
- 找到原表尾结点的前驱结点,并将它的后继指针指向新结点;
- 将新结点的前驱指针指向原表尾结点的前驱结点,并将后继指针指向NULL;
- 将原表尾结点的前驱结点指向NULL。
实现代码:
【👉🏻>>点击展开查看代码】
/**
* 删除表尾结点
*
* @author: Max Solider
* @date: 2022/10/8 20:38
* @param headNode
* @return org.example.linkedlist.dll.DllNode
*/
DllNode deleteTail(DllNode headNode) {
if (headNode == null || headNode.getNext() == null) {
headNode = null;
return headNode;
}
// 遍历找到表尾结点
DllNode tailNode = headNode;
while (tailNode.getNext() != null) {
tailNode = tailNode.getNext();
}
tailNode.getPrevious().setNext(null);
tailNode.setPrevious(null);
return headNode;
}
时间复杂度:
时间复杂度是O(n),用于遍历链表。
空间复杂度:
空间复杂度为O(1),用于保存临时变量。
删除链表中间的结点
核心思路:
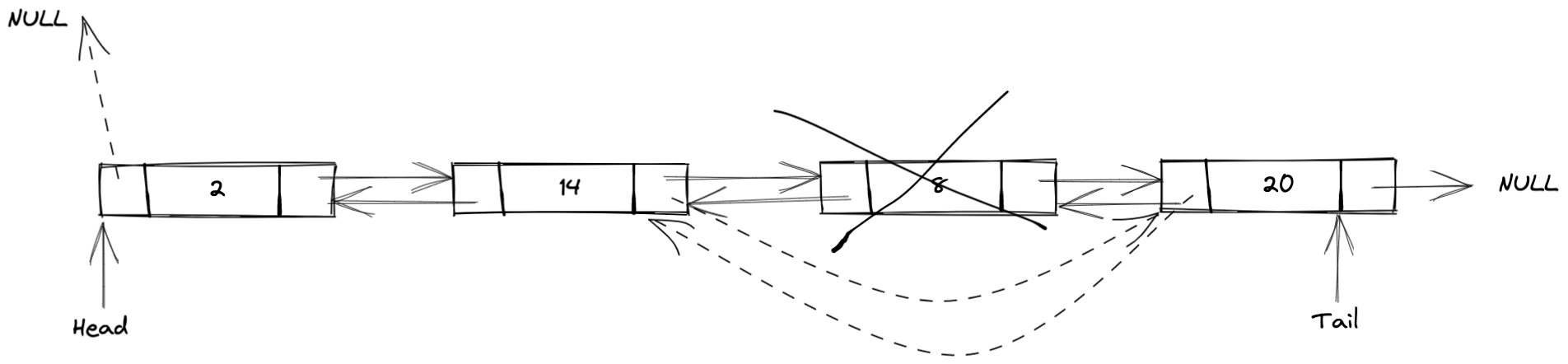
删除链表中间任意结点,包括以下5步:
- 判断删除位置合法性;
- 找到待删除位置;
- 找到待删除结点的前驱结点,将它的后继指针指向待删除结点的后继结点;
- 找到待删除结点的后继结点,将它的前驱指针指向待删除结点的前驱结点;
- 移除待删除结点,将它的前驱指针和后继指针都指向NULL。
实现代码:
【👉🏻>>点击展开查看代码】
/**
* 删除任意结点
*
* @author: Max Solider
* @date: 2022/10/8 20:58
* @param headNode
* @param position
* @return org.example.linkedlist.dll.DllNode
*/
DllNode delete(DllNode headNode, int position) {
if (headNode == null) {
return headNode;
}
if (position < 1) {
System.out.println("The position of node to delete is invalid. The position must be greater than 0");
return headNode;
}
// 找到待删除结点
DllNode deleteNode = headNode;
int count = 1;
while (count != position) {
deleteNode = deleteNode.getNext();
count++;
if (deleteNode == null) {
System.out.println("The position of node to delete is invalid. The position must be less than " + count);
return headNode;
}
}
// 更新待删除结点的前驱结点信息
if (deleteNode.getPrevious() != null) {
deleteNode.getPrevious().setNext(deleteNode.getNext());
} else {
// 如果删除的是表头结点,需要更新head指针
headNode = deleteNode.getNext();
}
// 更新待删除结点的后继结点信息
if (deleteNode.getNext() != null) {
deleteNode.getNext().setPrevious(deleteNode.getPrevious());
}
// 更新待删除结点信息
deleteNode.setPrevious(null);
deleteNode.setNext(null);
return headNode;
}
时间复杂度:
时间复杂度是O(n),用于遍历链表。
空间复杂度:
空间复杂度为O(1),用于保存临时变量。