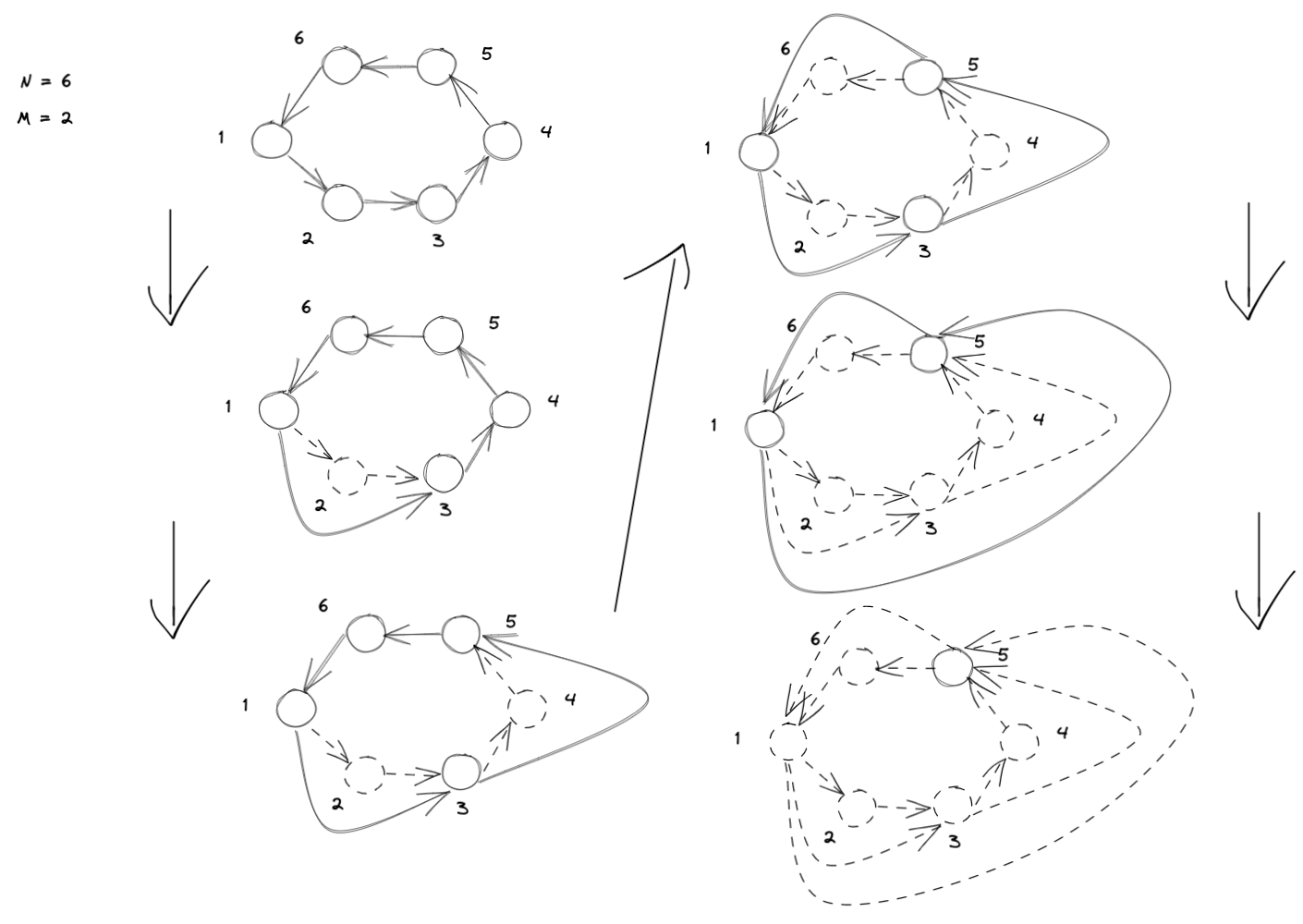
约瑟夫环问题
[!Tip]
本节源代码见Github链接🔗
问题描述
N个人想选出一个领头人,他们排成一个环,沿着环每数到第M个人就从环中排除该人,并从下一个人开始重新数。请找出最后留在环中的人。
核心思路
- 根据N生成环,并对每个结点进行编号
- 循环遍历环,剔除满足条件的结点,直到只剩下一个结点为止
实现代码
【👉🏻>>点击展开查看代码】
/**
* 找到约瑟夫环结点
*
* @param n 共n个人
* @param m 需要排除第m个结点
* @return 最后剩下的结点
*/
private static NormalListNode getJosephusPosition(int n, int m) {
if (n < 1) {
return null;
}
// 生成循环链表
NormalListNode head = new NormalListNode(1);
NormalListNode cur = head;
for (int i = 1; i < n; i++) {
cur.setNext(new NormalListNode(i + 1));
cur = cur.getNext();
}
cur.setNext(head);
// 获取约瑟夫环节点
return getJosephusPosition(head, m);
}
/**
* 找到约瑟夫环结点
*
* @param headNode 头结点
* @param m 需要排除第m个结点
* @return 最后剩下的结点
*/
private static NormalListNode getJosephusPosition(NormalListNode headNode, int m) {
if (headNode == null || headNode.getNext() == headNode) {
return headNode;
}
NormalListNode cur = headNode;
NormalListNode previous = null;
while (cur.getNext() != cur) {
int count = m;
while (--count > 0) {
previous = cur;
cur = cur.getNext();
}
previous.setNext(cur.getNext());
cur = cur.getNext();
}
return cur;
}
时间复杂度
时间复杂度为O(n),用于遍历链表。
空间复杂度
空间复杂度为O(1),用于存储临时变量。